「自然科学の統計学」を読む　～第4章最尤法 ③最尤推定量の最適性～

はじめに

東京大学教養学部統計学教室編「自然科学の統計学」は，1992年発行のやや古典的な文献であるが，自然科学に関わる統計学的テーマが簡潔にまとめられている。数理統計学の復習も兼ねて，本書を読むこととした。
ただ，基本的なことは他書で学んできたのと，本書自体がかなり細かく説明されているので，本書内の内容や数式を細かく追うというより，実務や統計検定の受験において有用そうなことを選んでまとめてみたい。

本記事は，「第4章最尤法」における，最尤推定量の最適性に関する読書メモである。

4.4 最尤推定量の最適性

本節では，最尤推定量が持つ各種性質について紹介している。この性質は，以下の3つである。

一致性 : 最尤推定量は(正則条件の下で)真の値 $\theta_0$ に確率収束する。
漸近有効性 : 最尤推定量の分散は， $n$ が大きいときに有効である(クラメール・ラオの下限に等しくなる)。
漸近正規性 : 最尤推定量がしたがう漸近分布は，正規分布にしたがう。

本記事では特に，漸近有効性・漸近正規性について説明する。

漸近分布の導出

一致性より， $n$ が大きいときに，最尤推定量 $\tilde{\theta}$ は真の値 $\theta_0$ に近づく。次に興味があるのは，

真の値の周りでのばらつきを知りたい。
区間推定・検定の問題を考える際に，期待値・分散だけでなく標本分布を知りたい。

ということである。

分散や標本分布について，順を追って説明する。

Step 1. 最尤推定量の定義式

データ $y_1, ..., y_n$ が，互いに独立に確率密度関数 $f_\theta(y)$ にしたがっているとき，最尤推定量の定義より，

$\begin{align} \left. \frac{\partial \log L(\theta)}{\partial \theta} \right| _{\theta = \tilde{\theta}} \equiv \left. \sum_{i=1}^n \frac{\partial \log f_{\theta}(y_i)}{\partial \theta} \right| _{\theta = \tilde{\theta}} =0 \\ \\ \end{align}$

が成り立つ(尤度方程式)。

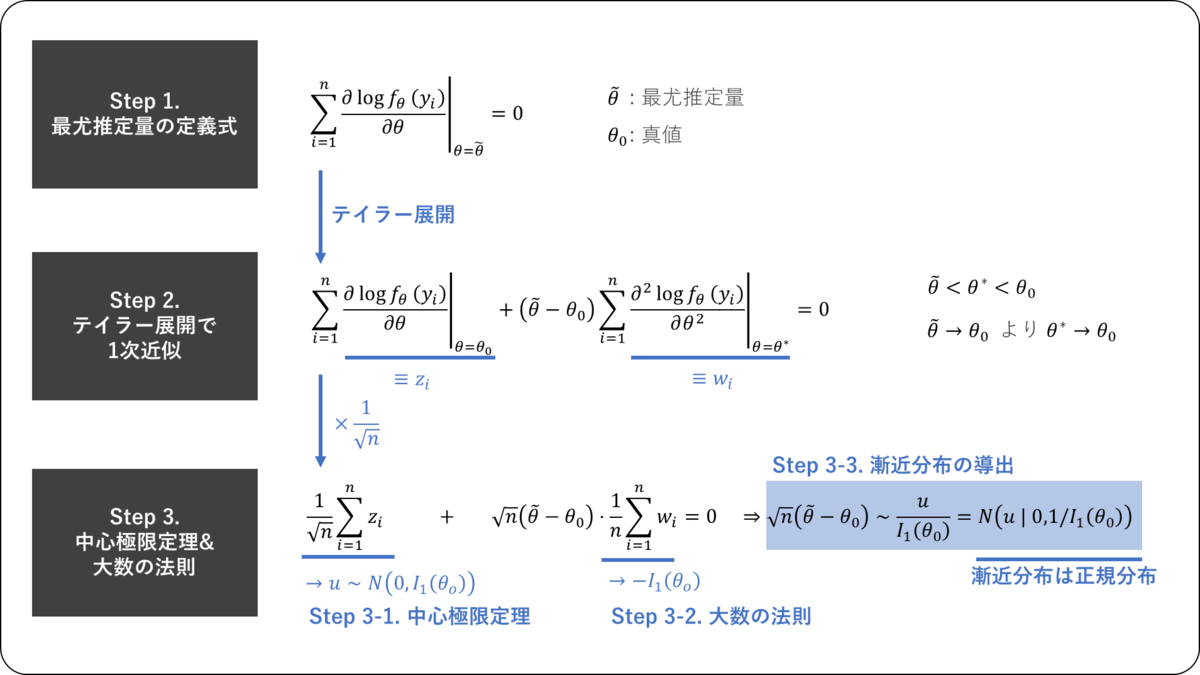
Step 2. テイラー展開で1次近似

尤度方程式の左辺を $\tilde{\theta}$ の関数とみなし，これを $\tilde{\theta} = \theta_0$ の周りでテイラー展開すると，

$\begin{align} \left. \sum_{i=1}^n \frac{\partial \log f_{\theta}(y_i)}{\partial \theta} \right| _{\theta = \theta_0} + (\tilde{\theta} - \theta_0) \left. \sum_{i=1}^n \frac{\partial^2 \log f_{\theta}(y_i)}{\partial \theta^2} \right| _{\theta = \theta^*} =0 \\ \\ \end{align}$

となる。ただし， $\theta^*$ は $\tilde{\theta}$ (最尤推定量)と $\theta_0$ (真値)の間の値であり， $(\theta^* - \tilde{\theta})(\theta^* - \theta_0) \lt 0$ を満たす。

$n$ を大きくすると， $\tilde{\theta}$ (最尤推定量)は $\theta_0$ (真値)に一致するので， $\theta^*$ も $\theta_0$ に一致する。

Step 3. 中心極限定理&大数の法則

$n$ が大きくなったときに，対数尤度の1階微分・2階微分の漸近的な性質を調べる。そのために，以下の $z_i, w_i$ を導入する。

$\begin{align} &z_i \equiv \left. \frac{\partial \log f_{\theta}(y_i)}{\partial \theta} \right| _{\theta = \theta_0}, \quad (i=1,...,n) \\ \\ &w_i \equiv \left. \frac{\partial^2 \log f_{\theta}(y_i)}{\partial \theta^2} \right| _{\theta = \theta^*}, \quad (i=1,...,n) \\ \\ \end{align}$

$y_i$ が独立に同一の分布にしたがうので， $z_i, w_i$ も独立に同一分布にしたがう。

次に，後々の解析のために，Step 2. の式を $\sqrt{n}$ で割る。

$\begin{align} \frac{1}{\sqrt{n}} \sum_{i=1}^n z_i + \sqrt{n} (\tilde{\theta} - \theta_0) \cdot \frac{1}{n} \sum_{i=1}^n w_i = 0 \\ \\ \end{align}$

Step 3-1. 中心極限定理の利用(対数尤度の1階微分の解析)

対数尤度の1階微分の解析を行なうために，中心極限定理を用いる。

中心極限定理は，確率変数 $X_i (i=1,...,n)$ が互いに独立かつ同一の確率分布に従う確率変数列で， $E(X_i)=\mu, V(X_i)=\sigma^2$ のとき，

$\begin{align} P \left( \frac{ \bar{X} - \mu}{ \sigma/\sqrt{n} } \leq x \right) =P \left( \frac{ \sum X_i - n \mu}{ \sqrt{n} \sigma } \leq x \right) \rightarrow \Phi(x) \quad (n \rightarrow \infty) \\ \\ \end{align}$

が成り立つ，という定理である(ここで， $\bar{X}$ は $X_i$ の平均， $\Phi(x)$ は標準正規分布の累積分布関数)。
中心極限定理を書き換えると， $n \rightarrow \infty$ において，

$\begin{align} \frac{ \sum X_i - n \mu}{ \sqrt{n} \sigma} \sim \mathcal{N}(0, 1) \Leftrightarrow \frac{ \sum X_i - n \mu}{ \sqrt{n}} \sim \mathcal{N}(0, \sigma^2) \\ \\ \end{align}$

となる。

$z_i$ は対数尤度の1階微分であるため，

$\begin{align} E(z_i) &= E_{\theta_0} \left[ \left. \frac{\partial \log f_{\theta}(y_i)}{\partial \theta} \right| _{\theta = \theta_0} \right] = 0 \\ \\ V(z_i) &= E_{\theta_0} \left[ \left( \left. \frac{\partial \log f_{\theta}(y_i)}{\partial \theta} \right| _{\theta = \theta_0} \right)^2 \right] = I_1(\theta_0) \\ \\ \end{align}$

となる。ここで $I_1(\theta_0)$ は，サンプル1つ分のフィッシャー情報量である。

これらと中心極限定理を用いると， $n \rightarrow \infty$ のとき，

$\begin{align} \frac{1}{ \sqrt{n} } \sum_{i=1}^n z_i \rightarrow _d \mathcal{N}(0, I_1(\theta_0)) \\ \\ \end{align}$

となる。

Step 3-2. 大数の法則の利用(対数尤度の2階微分の解析)

対数尤度の2階微分の解析を行なうために，大数の法則を用いる。

$w_i$ は対数尤度の2階微分であるため，期待値はサンプル1個分のフィッシャー情報量に $-1$ を掛けたものになる。すなわち，

$\begin{align} E_{\theta_0} (w_i) = -1 \times E_{\theta_0} \left[ \left. - \frac{\partial^2 \log f_{\theta}(y_i)}{\partial \theta^2} \right| _{\theta = \theta_0} \right] = -I_1(\theta_0) \\ \\ \end{align}$

となる。

大数の法則より， $n \rightarrow \infty$ の極限において，平均は期待値に収束する。またこのとき， $\theta^* \rightarrow \theta_0$ になるので，

$\begin{align} \frac{1}{n} \sum_{i=1}^n w_i \rightarrow E_{\theta_0} \left[ \left. \frac{\partial^2 \log f_{\theta}(y_i)}{\partial \theta^2} \right| _{\theta = \theta_0} \right] = -I_1(\theta_0) \\ \\ \end{align}$

となる。

Step 3-3. 漸近分布の導出

Step 3-1. およびStep 3-2. の結果をまとめると， $n$ が大きいとき，

$\begin{align} &u \equiv \frac{1}{\sqrt{n}} \sum_{i=1}^n z_i \rightarrow _d \mathcal{N}(0, I_1(\theta_0)) \\ \\ &\sqrt{n} (\tilde{\theta} - \theta_0) \cdot \frac{1}{n} \sum_{i=1}^n w_i \rightarrow -I_1(\theta) \\ \\ \therefore & \sqrt{n} (\tilde{\theta} - \theta_0) \sim \frac{u}{I_1(\theta_0)} = \mathcal{N}(0, 1/ I_1(\theta_0)) \\ \\ \end{align}$

となり，最尤推定量の漸近分布が得られる。

またこの式より，

$\begin{align} \tilde{\theta} \sim \mathcal{N}(0, 1/ n I_1(\theta_0)) \\ \\ \end{align}$

とも書けるが，このことより漸近分散がクラメール・ラオの下限に等しいので，最尤推定量は漸近的に有効な推定量であると言える。

まとめと感想

今回は，「第4章最尤法」における，最尤推定量の最適性についてまとめた。

漸近正規性の導出は，尤度方程式のテイラー展開を起点に，中心極限定理と大数の法則を組み合わせて，最尤推定量の極限分布を得る流れとなっている。この過程をステップごとに追うことで，最尤推定量がなぜ「漸近的に正規分布に従うのか」が論理的に理解できる。そしてその分散がフィッシャー情報量の逆数となり，クラメール・ラオの下限を達成することで「漸近有効性」が保証される。

ここで重要なのは、最尤推定が「ただ便利な推定方法」なのではなく，数学的に最適性を備えた推定量である，という位置づけである。サンプルサイズが有限のときには必ずしも最適ではないが，大標本の極限においては一貫して信頼できる性質をもつ点が，理論・実務の両面で強力な裏付けとなる。

統計検定1級対策としては，この「漸近正規性」と「漸近有効性」を論証するための典型的な流れ(テイラー展開 → 中心極限定理 → 大数の法則 → フィッシャー情報量の導入)を理解しておくことが非常に重要である。特に， $1/\sqrt{n}$ で割ることで中心極限定理を使えるようにする，といったテクニックは，他の漸近分布を考えるうえでも有用であろう。