はじめに
製造業のデータサイエンス実務では,統計的手法や機械学習・深層学習モデルを適切に組合わせて,現場で再現性の高い意思決定を支えることが求められる。とりわけ近年は,深層学習の発展により手法の多様化が進んでいるため,機械学習・深層学習を体系的に理解することは,現場の課題定義やモデリング戦略の質を大きく左右する。
持橋大地・鈴木大慈 監訳「確率的機械学習 入門編II」は,世界的に評価の高いK.P.Murphy著 "Probabilistic Machine Learning (Book1)" の和訳であり,確率モデルに基づく機械学習,深層学習といった基礎が丁寧に整理されている。私は統計検定1級として数理統計の基礎は学んできたが,機械学習・深層学習は実務に応じて場当たり的に学んできた。実務での応用に向けて,機械学習・深層学習の基礎を体系的に学び,チームの技術力を底上げしたいと考えている。また読書メモに自身の理解をまとめることで,製造業に携わる若いエンジニアにとっても有益な知識を還元できればと考えている。
※なおボリュームが多い本なので,知っているところは端折りながら読み進めたい。
本記事は,「第13章 構造化データのためのニューラルネットワーク」における,ニューラルネットワークの訓練に関する読書メモである。
13.5 正則化
本節では,DNNの学習における過剰適合を防ぐ方法について説明している。
巨大なニューラルネットワークは,パラメータ数が数百万個を簡単に超えてしまうので,過剰適合の帽子は重要である。
13.5.1 早期停止
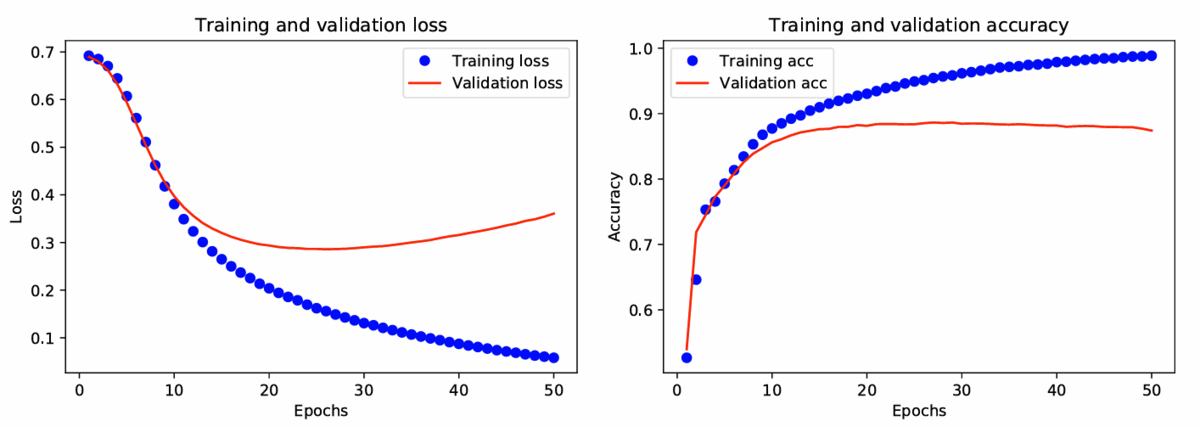
早期停止(early stopping)と呼ばれるヒューリスティックは,過剰適合を防ぐための最も簡単な方法である。
これは,検証データ集合における誤差が増加し始めた時点で学習手続きを打ち切るものである。
13.5.2 重み減衰
過剰適合を防ぐ別の方法として,パラメータに事前分布,たとえば
- 重み :
- バイアス :
のように,設定する方法がある。
これは目的関数にL2正則化を施すのと等価である。この方法を重み減衰(weight decay)と呼ぶ。
13.5.3 疎なDNN
ニューラルネットワークに対して,L1正則化やARDを用いて疎な解を得る方法がある。しかしGPUは密な行列計算に最適化されているため,重み疎行列であることは計算上の利益がない。
それでも,変数グループのスパース性を奨励する方法を用いると,モデル中の層全体を枝刈りすることができる。結果として,計算速度の向上やメモリ使用量の削減につながる。
13.5.4 ドロップアウト(間引き)法
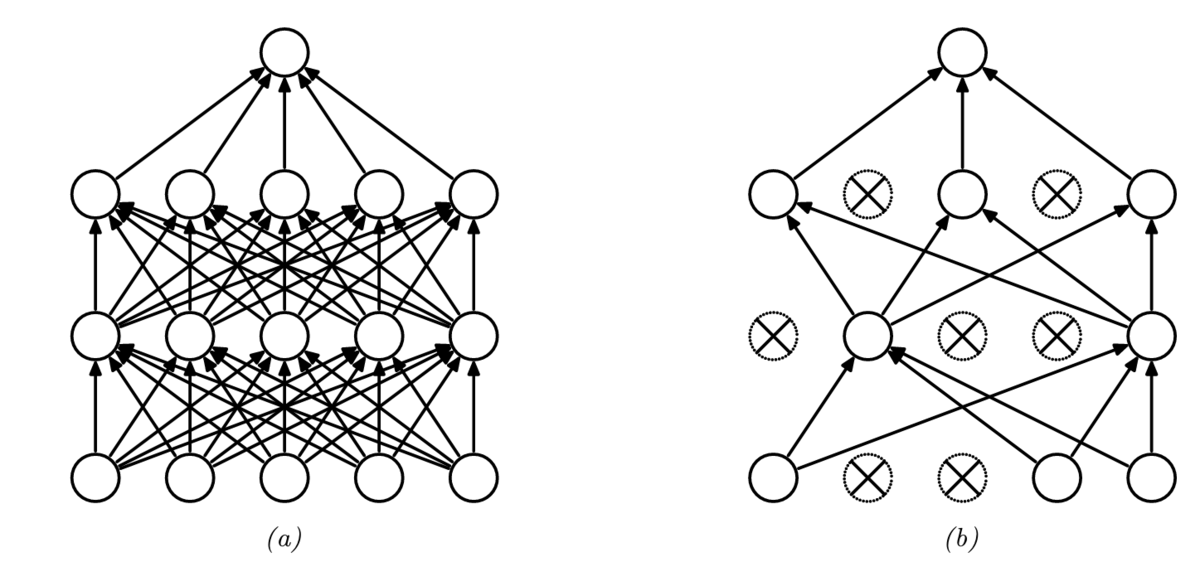
各ニューロンからの出力接続を確率でランダムに切る方法をドロップアウト(dropout, 間引き)と呼ぶ。
ドロップアウトは,過剰適合を劇的に減らす効果があり,広く利用されている。
13.5.5 ベイズ的ニューラルネットワーク
巨大なモデルだと,得られるデータ点数よりもパラメータ数の方が多くなる。そのため,訓練データに対して同じくらいよく適合しながら,異なった汎化をするモデルが複数存在する可能性がある。
この事後予測分布の不確実性を捉えておくことが有益な場合が多い。そのためには,
13.5.6 (確率的)勾配降下法の正則化効果
前項までは、正則化を実現するための各種手法を説明していたが、本稿では、(確率的)勾配降下法という手法自体が持つ正則化の効果について説明している。
平坦最小解と陰的な正則化
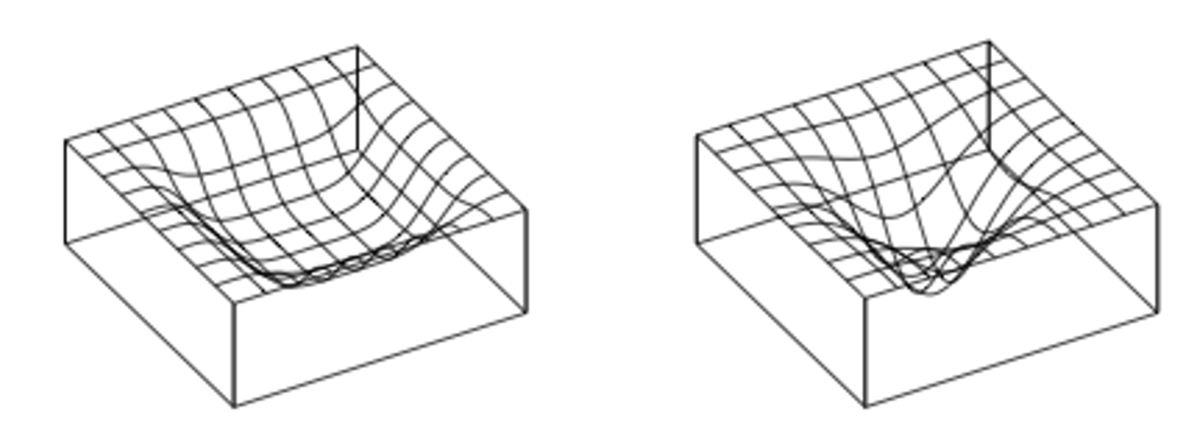
経験損失最小化の観点では、損失関数は「局所的だが深い『穴』を持つ」、すなわち局所的だが損失が非常に小さいパラメータ集合を尖鋭最小解見つけるような最適化アルゴリズムが良いとされる。
一方でこのような解は、訓練データに過適合したようなモデルになっている。
そのためモデルの学習としては、平坦最小解を目指すべきとされる。
このような領域に存在する解は、入力の変動に頑健で良好な汎化性能を持つことが多い。
平坦最小解は、パラメータの張る空間の中でも、事後分布の不確定性が大きい領域に対応している。
SGDで付加されているノイズ成分は、局所的な探索範囲に侵入することを防ぐため、平坦最小解に到達しやすい。
このことは、陰的な正則化(implicit regularization)と呼ばれる。
データによる損失曲面の変動
損失曲面(損失関数がなす曲面)は,パラメータ値だけではなく,データによっても変動する。
これは,通常は全パッチを利用した勾配降下は難しいので,ミニバッチごとに損失曲線の集合を用いることになるためである。
平坦最小解が得られるとき,ミニバッチごとの損失曲面の状態は以下の2パターンが考えられる。
- おのおののカーブが「盆地」に対応した場合(下図の(a))
- 多数の異なる狭い「盆地」を平均した結果として全体的には広い盆地を得た場合(下図の(b))
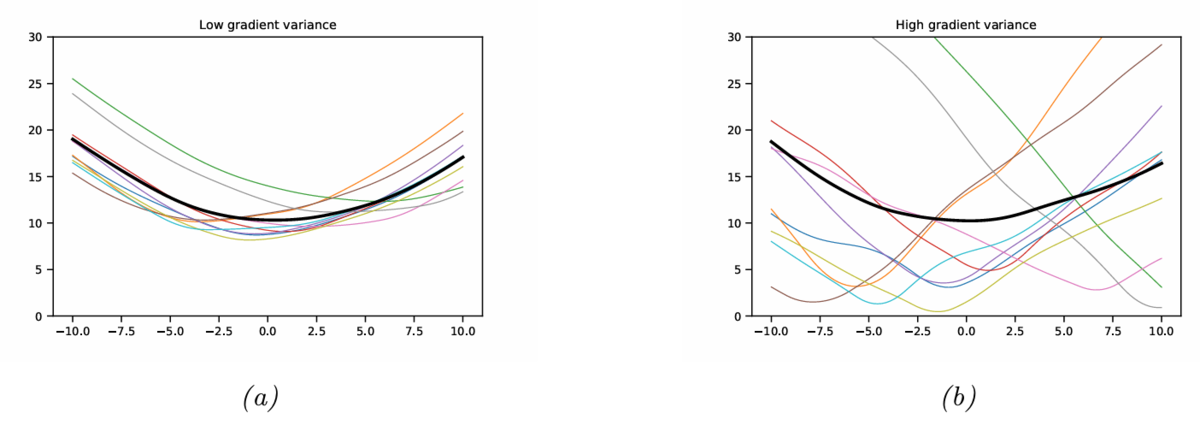
Figure 13.20の(a)の状態であれば,パラメータ空間内でも摂動に頑健な,良く汎化する解だと考えられる。
一方で(b)の状態であれば,得られたパラメータ推定結果は,それほど汎化しない可能性が高い。
13.5.7 過剰パラメーターモデル
最近のニューラルネットワークは,訓練サンプル数よりもパラメータ数
の方が多いことがある。このようなモデルは過剰パラメータ(over-parametrized)である,と呼ばれる。
通常は,パラメータの数が増えると過剰適合を起こし,テスト誤差が大きくなる。しかし,の場合,
を増加し続けるとテスト誤差が再び減少する。これは二重降下(double descent)という現象である。
まとめと感想
今回は,「第13章 構造化データのためのニューラルネットワーク」における,正則化についてまとめた。
確率的勾配降下法の正則化効果
確率的勾配降下法(SGD)は,ミニバッチを用いることで計算量の多さに対応する方法であるが,SGD自体が正則化の効果を持つ,というのは興味深かった。
これは,SGDが計算量の観点でも,安定したパラメータ推定という観点でも有利である,ということであり,この手法の有効性が改めて確認できた。
従来の常識を覆す過剰パラメータモデル
深層学習以前の機械学習では,多すぎるパラメータは過剰適合を起こす,ということがよく知られていた。
一方で深層学習の場合,パラメータが多すぎる場合でもテスト誤差が減る「二重降下」が起きる。
これは,従来の機械学習の常識を覆すことであり,衝撃的であった。
深層学習の特徴については,今泉 允聡 著「深層学習の原理に迫る」にまとめられており,過去に読書メモもまとめたことがあるので,改めて見返したい。
stern-bow.hatenablog.com
本記事を最後まで読んでくださり,どうもありがとうございました。
参考サイト
- 確率的機械学習:入門編 II |朝倉書店
- 『確率的機械学習:入門編』サポートサイト
- 原著関連
- Probabilistic Machine Learning: An Introduction : 原著のサポートページ
- pyprobml/notebooks.md at auto_notebooks_md · probml/pyprobml · GitHub : 原著の図作成用Notebooks一覧