「スモールデータ解析と機械学習」を読む　～第3章回帰分析と最小二乗法 ②多重共線性の問題～

はじめに

藤原幸一著「スモールデータ解析と機械学習」は，サンプル数が少ない状況でのモデル構築や予測精度の確保，統計的な不確実性の扱い方など，現場で直面する悩みに直結する理論と実践がコンパクトにまとまっている。製造業のデータ解析において「少ないデータだから仕方ない」と諦めるのではなく，「少ないからこそできる工夫」を身につけるためにこの本を読み，その学びをブログで共有しようと思う。

本記事は，「第3章回帰分析と最小二乗法」における，多重共線性の問題に関する読書メモである。

3.7 多重共線性の問題

本節では，最小二乗法を用いるときに問題になる多重共線性について説明している。多重共線性の問題には，変数間の相関関係と，最小二乗解が含む逆行列の性質がかかわっている。

本節では，多重共線性が最小二乗法に与える悪影響を，行列の逆行列計算と特異値分解の視点から解説している。

多重共線性の本質
説明変数間に強い相関があると，データ行列 $\boldsymbol{X}$ の列ベクトルがほぼ線形従属となり $\boldsymbol{X}^T \boldsymbol{X}$ のランクが小さくなる。完全に従属すれば逆行列は存在しない。また，わずかにノイズが混じれば，逆行列は存在するが極めて不安定になる。

悪条件と条件数
この不安定性は「悪条件（ill-conditioned）」と呼ばれ，最大特異値 $\sigma_{\mathrm{max}}$ と最小特異値 $\sigma_{\mathrm{min}}$ の比 $\kappa(\boldsymbol{A}) = \sigma_{\mathrm{max}} / \sigma_{\mathrm{min}}$ で定量化される。多重共線性が強いほど $\sigma_{\mathrm{min}}$ が小さくなり、条件数は大きくなる。

特異値分解から見る影響
$(\boldsymbol{X}^T \boldsymbol{X})^{-1}$ は特異値の逆数の二乗を含むため，最小特異値が極端に小さい場合，ノイズによって推定結果 $\hat{\boldsymbol{\beta}}$ が大きく変動する。これが多重共線性による推定不安定性の数学的理由である。

逆行列とノイズ

以下の行列 $\boldsymbol{C}$ を考える。

$\begin{align} \boldsymbol{C} = \begin{bmatrix} 2 & 1 \\ 4 & 2 \\ \end{bmatrix} \\ \\ \end{align}$

この行列について，1列目のベクトルは２列目のベクトルの定数倍になっており，フルランクではないため，逆行列を持たない。

この行列 $\boldsymbol{C}$ の要素に，ノイズが含まれる行列 $\boldsymbol{A}$ および $\boldsymbol{B}$ が得られたとする。

$\begin{align} \boldsymbol{A} = \begin{bmatrix} 2.01 & 1 \\ 4 & 2.01 \\ \end{bmatrix} , \quad \boldsymbol{B} = \begin{bmatrix} 1.99 & 1 \\ 4 & 2.02 \\ \end{bmatrix} \\ \\ \end{align}$

これらの逆行列を求めると，以下のようになる。

$\begin{align} \boldsymbol{A}^{-1} = \begin{bmatrix} 50.12 & -24.94 \\ -99.75 & 50.12 \\ \end{bmatrix} , \quad \boldsymbol{B}^{-1} = \begin{bmatrix} 102.02 & -50.50 \\ -202.02 & 100.50 \\ \end{bmatrix} \\ \\ \end{align}$

このように，本来ならばランクが落ちている行列にノイズが混入したため逆行列を持つようになった場合，逆行列を求めようとすると，わずかなノイズの違いで結果が大きくばらつく。

条件数

逆行列が大きくばらつく状況を悪条件(ill-conditioned)という。悪条件であるかどうかは，条件数と呼ばれるコンピュータでの数値解析のしやすさの尺度によって求める。

行列 $\boldsymbol{A}$ の条件数 $\kappa(\boldsymbol{A})$ は，行列 $\boldsymbol{A}$ の最大特異値 $\sigma_{\mathrm{max}}$ と最小特異値 $\sigma_{\mathrm{min}}$ の比として， $\kappa(\boldsymbol{A}) = \sigma_{\mathrm{max}} / \sigma_{\mathrm{min}}$ で定義される。

ランクが落ちている行列では最小特異値が0になるため，条件数は無限大となる。

最小二乗解と多重共線性に関する考察

本書の説明に基づき，最小二乗解と多重共線性について考察してみた。

最小二乗解は以下のように与えられる。

$\begin{align} \hat{\boldsymbol{\beta} } = (\boldsymbol{X}^T \boldsymbol{X})^{-1} \boldsymbol{X}^T \boldsymbol{y} \\ \\ \end{align}$

最小二乗解に含まれる逆行列は $(\boldsymbol{X}^T \boldsymbol{X})^{-1}$ である。この逆行列を，特異値分解を用いて確認する。特異値分解を用いると， $\boldsymbol{X} = \boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^T$ なので，

$\begin{align} (\boldsymbol{X}^T \boldsymbol{X}) &= (\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^T)^T (\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{V}^T) \\ \\ &= \boldsymbol{V} \boldsymbol{\Sigma}^2 \boldsymbol{V}^T \\ \\ &=\boldsymbol{V} \begin{bmatrix} \sigma_1^2 & & \\ & \ddots & \\ & & \sigma_M^2 \\ \end{bmatrix} \boldsymbol{V}^T \\ \\ \end{align}$

となる。

ここで $\boldsymbol{V}$ は正規直交基底であるため， $\boldsymbol{V}^T = \boldsymbol{V}^{-1}$ となる。そのため，

$\begin{align} (\boldsymbol{X}^T \boldsymbol{X})^{-1} &= (\boldsymbol{V} \boldsymbol{\Sigma}^2 \boldsymbol{V}^T)^{-1} \\ \\ &= \boldsymbol{V} \boldsymbol{\Sigma}^{-2} \boldsymbol{V}^T \\ \\ &=\boldsymbol{V} \begin{bmatrix} \sigma_1^{-2} & & \\ & \ddots & \\ & & \sigma_M^{-2} \\ \end{bmatrix} \boldsymbol{V}^T \\ \\ \end{align}$

であることが分かる。

ここで， $\boldsymbol{X}$ に多重共線性があるとすると， $\boldsymbol{X}$ の列ベクトルの間の相関が大きくなる。
そのため，このような列ベクトル群は，少数のローディングベクトルで代表されるようになり，このローディングベクトルに直行するようなローディングベクトルの影響度が小さくなる。
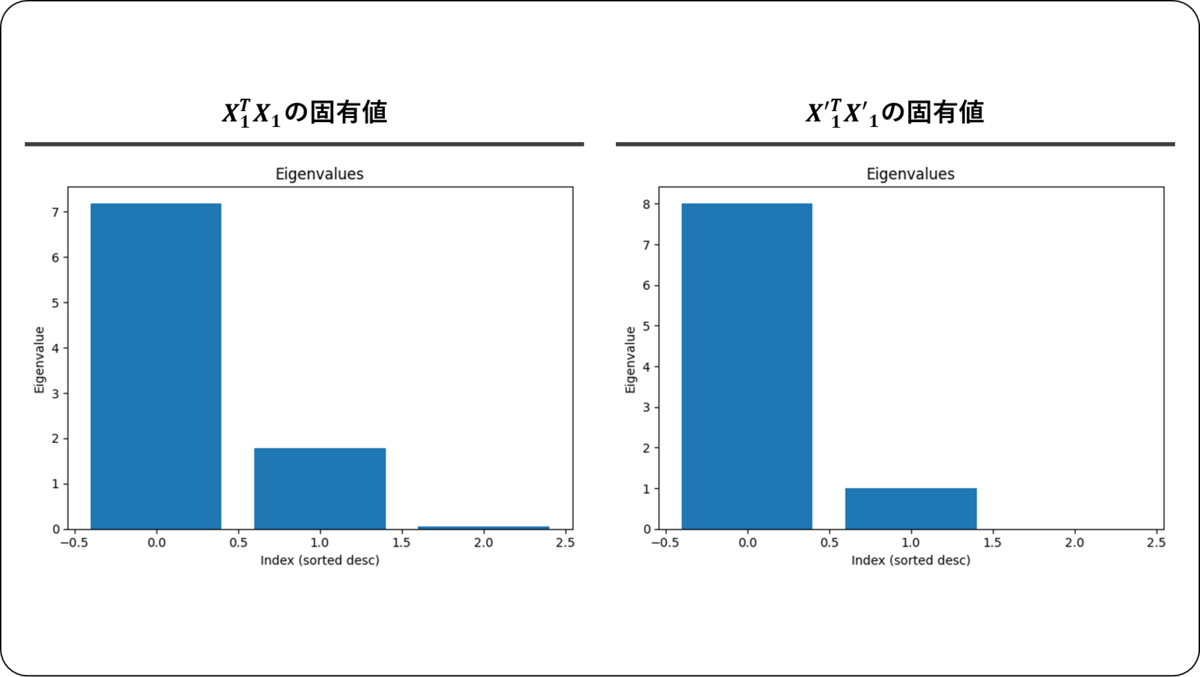
すなわち，上位固有値の値が大きくなり，下位固有値の値はとても小さい値になる。

このとき，逆行列 $(\boldsymbol{X}^T \boldsymbol{X})^{-1}$ の式に現れる下位固有値の逆数が変動しやすくなり，ノイズの違いで結果が大きくばらつくことがわかる。

なお条件数は，最大特異値と最小特異値の比で表されるので，多重共線性があるときには条件数が大きくなるということが分かる。

数値実験

本書P64～68において，多重共線性があるデータと無いデータで，回帰係数を比較していた。本記事では，同じデータを用いて，固有値の大きさを確認した。

多重共線性が無いデータ

$\begin{align} \boldsymbol{X}_1 = \begin{bmatrix} 0.01 & 0.50 & -0.12 \\ 0.97 & -0.63 & 0.02 \\ 0.41 & 1.15 & -1.17 \\ -1.38 & -1.02 & 1.27 \\ \end{bmatrix} \\ \\ \end{align}$

と，多重共線性の問題があるデータ

$\begin{align} \boldsymbol{X}_1' = \begin{bmatrix} -1.12 & -0.51 & 0.69 \\ -0.43 & -1.612 & 1.02 \\ 0.37 & 1.10 & -0.98 \\ 1.19 & 0.53 & -0.73 \\ \end{bmatrix} \\ \\ \end{align}$

について，それぞれ $\boldsymbol{X}_1^T \boldsymbol{X}_1$ および $\boldsymbol{X}_1'^T \boldsymbol{X}_1'$ を計算し，この固有値の棒グラフを作成した結果は下図のようになる。

右図である $\boldsymbol{X}_1'^T \boldsymbol{X}_1'$ の固有値について，第3固有値の値が他の固有値に比べて極めて小さいことが確認できた。このように多重共線性の問題があるデータの場合，下位固有値の値が小さくなる。

まとめと感想

今回は，「第3章回帰分析と最小二乗法」における，多重共線性の問題についてまとめた。

製造業の現場データは，測定項目が多く工程間に依存関係が強いため，多重共線性が発生しやすい。例えば温度・圧力・速度のように制御盤で同時に変化させるパラメータや，加工後の複数寸法が同じ要因で変動するケースでは， $\boldsymbol{X}^T \boldsymbol{X}$ が悪条件化するのは避けられない。

この節で印象的なのは，単なる「相関が高いと危ない」ではなく，特異値分解での固有値の偏りとしてその不安定性を説明している点だ。これにより条件数を実際に計算して診断できるし，「どの軸の情報が弱いか」を特定できる。

実務的には，この後の節の内容にもかかわってくるが，