「ベイズ最適化」を読む　～第2章ブラックボックス関数のベイズモデリング ①ベイズ線形回帰モデル～

$\begin{align} y_i &= \boldsymbol{w}^T \boldsymbol{\phi} (\boldsymbol{x}_i) + \varepsilon_i \\ \\ \varepsilon &\sim \mathcal{N}(0, \sigma^2) \\ \end{align}$

と表す。ただし， $\phi$ は基底関数である。

上式を確率分布の形で表すと，

$\begin{align} y_i \sim p(y_i | \boldsymbol{\phi} (\boldsymbol{x}_i), \boldsymbol{w}) = \mathcal{N}(\boldsymbol{w}^T \boldsymbol{\phi} (\boldsymbol{x}_i), \sigma^2) \\ \end{align}$

となる。

$n$ 個の観測データ $\mathcal{D}_n$ が得られた時の尤度は，

$\begin{align} p(\boldsymbol{y} | \boldsymbol{X}, \boldsymbol{w}, \sigma) = \frac{1}{ (\sqrt{2 \pi} \sigma)^n } \exp \left\{ -\frac{1}{2 \sigma^2} || \boldsymbol{y} - \boldsymbol{\Phi} \boldsymbol{w} || ^2 \right\} \\ \end{align}$

となる。

ベイズ線形回帰モデル

ベイズ線形回帰モデルは，モデルパラメータ $\boldsymbol{w}$ に確率分布を設定したモデルである。ベイズ線形回帰モデルにおいて興味があることは，主に以下の2つである。

学習データから，モデルパラメータ $\boldsymbol{w}$ の事後分布を推定する
新しい入力 $\boldsymbol{x}_*$ が得られたときに，学習結果を用いて出力 $y_*$ の予測分布を算出する

である。

2.について，予測分布のグラフィカルモデルは以下の通りである。

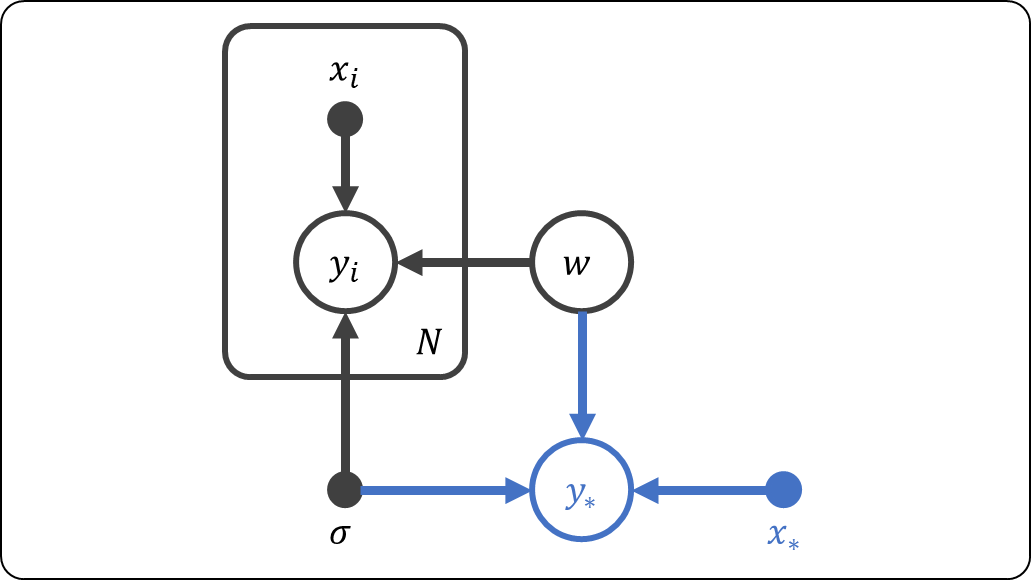
予測分布は，以下の式で表される。

$\begin{align} p(y_* | \boldsymbol{\Phi}, \boldsymbol{y}, \boldsymbol{x}_*) = \int p(y_* | \boldsymbol{\phi}(\boldsymbol{x}_*), \boldsymbol{w}) p(\boldsymbol{w} | \boldsymbol{\Phi}, \boldsymbol{y}) d \boldsymbol{w} \\ \end{align}$

この式は，左辺を $\boldsymbol{w}$ を加えて同時分布にして， $\boldsymbol{w}$ を積分消去することで得られるが，各項を分解して考えると意味が理解しやすい。

モデルパラメータの事後分布 $p(\boldsymbol{w} | \boldsymbol{\Phi}, \boldsymbol{y})$ から，乱数 $\boldsymbol{w}$ を生成(サンプリング)する。
この $\boldsymbol{w}$ を回帰係数とした線形モデルを構築し， $p(y_* | \boldsymbol{\phi}(\boldsymbol{x}_*), \boldsymbol{w})$ を算出する。
上記2つのステップを複数回繰り返して，平均化する。

尤度やモデルパラメータがしたがう分布が正規分布であれば，予測分布も正規分布になる。

数値実験

本書P30 図2.4を参考に，ベイズ線形回帰モデルを実装した。

真の関数を $y = x - 0.5$ として，観測ノイズを加えた30点のデータを学習用データとした。
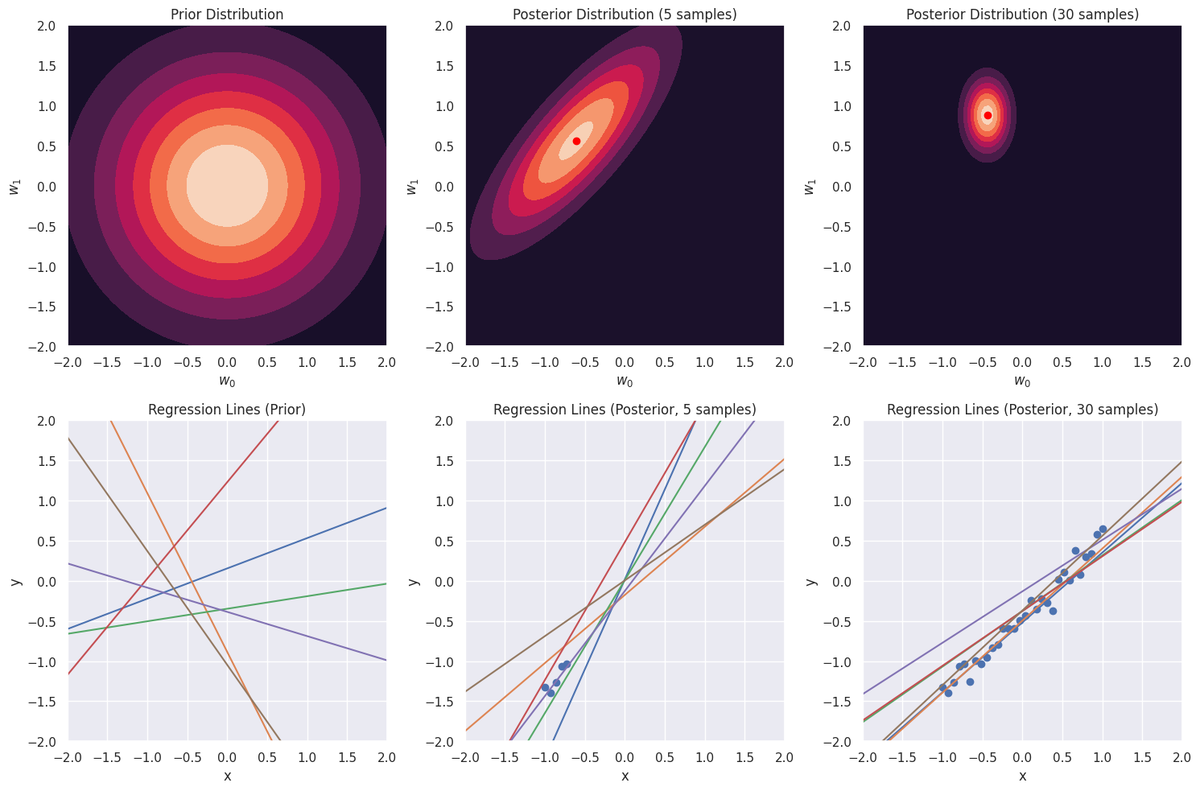
学習用データを全く与えない場合(事前分布に相当)と，学習用データを5点サンプルして与えた場合と，学習用データを30点すべて用いた場合で，事後分布と回帰直線を作成した。

左上は，モデルパラメータ(切片 : $w_0$ ，傾き : $w_1$ )に学習用データの情報が含まれないので，どちらも平均が0になっている。
左下は，事前分布が生成するモデルパラメータである。平均0，分散共分散行列が $\mathrm{diag}(1, 1)$ の多変量正規分布にしたがう値がモデルパラメータになっているので，傾きが負になっているものも存在する。

中上は，学習用データを5点サンプルして与えた場合のモデルパラメータの事後分布である。分散共分散行列の楕円が事前分布よりは小さくなっている。
中下は，学習用データを5点サンプルして与えた場合のモデルパラメータの事後分布から得られたモデルパラメータを用いて作成した回帰直線である。

右上は，学習用データ30点をすべて用いた場合のモデルパラメータの事後分布である。分散共分散行列の楕円がさらに小さくなり，値が絞られていることが確認できる。
右下は，学習用データ30点をすべて用いた場合のモデルパラメータの事後分布から得られたモデルパラメータを用いて作成した回帰直線である。

学習用データのサンプル数が増えるほど，事後分布の分散が小さくなっていることが確認できる。

上記の分析用pythonコードはこちら。

クリックで展開

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
import seaborn as sns

# データ生成
np.random.seed(0)
n_data = 30
x = np.linspace(-1.0, 1.0, n_data)
y = 1.0 * x - 0.5 + 0.1 * np.random.randn(n_data)

# 事前分布のパラメータ
mu0 = np.array([0.0, 0.0])
Sigma0 = np.array([[1.0, 0.0], [0.0, 1.0]])

# 事後分布の計算
def posterior(x, y, mu0, Sigma0, beta):
    n = len(x)
    X = np.vstack((np.ones(n), x))
    SigmaN = np.linalg.inv(np.linalg.inv(Sigma0) + beta * X @ X.T)
    muN = SigmaN @ (np.linalg.inv(Sigma0) @ mu0 + beta * X @ y)
    return muN, SigmaN

# グラフ描画
sns.set()  # seabornスタイルを設定
fig, axes = plt.subplots(2, 3, figsize=(15, 10))

xnew = np.linspace(-2.0, 2.0, n_data)

# (1, 1) 事前分布の等高線
x_w0 = np.linspace(-2, 2, 100)
x_w1 = np.linspace(-2, 2, 100)
X_w0, X_w1 = np.meshgrid(x_w0, x_w1)
pos = np.empty(X_w0.shape + (2,))
pos[:, :, 0] = X_w0
pos[:, :, 1] = X_w1
rv = multivariate_normal(mu0, Sigma0)
axes[0, 0].contourf(X_w0, X_w1, rv.pdf(pos))
axes[0, 0].set_xlabel('$w_0$')
axes[0, 0].set_ylabel('$w_1$')
axes[0, 0].set_xlim(-2.0, 2.0)
axes[0, 0].set_ylim(-2.0, 2.0)
axes[0, 0].set_title('Prior Distribution')

# (2, 1) 事前分布から予測される回帰直線
for i in range(6):
  w = np.random.multivariate_normal(mu0, Sigma0)
  y_pred = w[0] + w[1]*xnew
  axes[1, 0].plot(xnew, y_pred)
#axes[1, 0].scatter(x, y)
axes[1, 0].set_xlabel('x')
axes[1, 0].set_ylabel('y')
axes[1, 0].set_xlim(-2.0, 2.0)
axes[1, 0].set_ylim(-2.0, 2.0)
axes[1, 0].set_title('Regression Lines (Prior)')

beta = 1.0

for i, n_samples in enumerate([5, n_data]):
  # 事後分布計算
  muN, SigmaN = posterior(x[:n_samples], y[:n_samples], mu0, Sigma0, beta)

  # (1, 2) or (1, 3) 事後分布の等高線
  rv = multivariate_normal(muN, SigmaN)
  axes[0, i+1].contourf(X_w0, X_w1, rv.pdf(pos))
  axes[0, i+1].scatter(muN[0], muN[1], c='red')
  axes[0, i+1].set_xlabel('$w_0$')
  axes[0, i+1].set_ylabel('$w_1$')
  axes[0, i+1].set_xlim(-2.0, 2.0)
  axes[0, i+1].set_ylim(-2.0, 2.0)
  axes[0, i+1].set_title(f'Posterior Distribution ({n_samples} samples)')

  # (2, 2) or (2, 3) 事後分布から予測される回帰直線
  for _ in range(6):
    w = np.random.multivariate_normal(muN, SigmaN)
    y_pred = w[0] + w[1]*xnew
    axes[1, i+1].plot(xnew, y_pred)
  axes[1, i+1].scatter(x[:n_samples], y[:n_samples])
  axes[1, i+1].set_xlabel('x')
  axes[1, i+1].set_ylabel('y')
  axes[1, i+1].set_xlim(-2.0, 2.0)
  axes[1, i+1].set_ylim(-2.0, 2.0)
  axes[1, i+1].set_title(f'Regression Lines (Posterior, {n_samples} samples)')

plt.tight_layout()
plt.show()