一様分布の最尤推定～尤度方程式の罠～ #統計検定

はじめに

統計検定１級の2019年統計数理問3において，連続一様分布(以下，単に「一様分布」と記載する)の問題が出題された。一様分布について，問題集で「一様分布の最尤推定」という問題があり，つまずいたことがあったので，考え方を整理した。

最尤推定

最尤推定は，統計モデルのパラメータ推定手法ではおなじみの方法で，機械学習でも登場する手法である。
パラメータ $\theta$ を持つ確率密度関数 $f(x| \theta)$ について，データ $X = (X_1, ..., X_n)$ が与えられているときに，尤度関数

$\displaystyle L(\theta | X) = \prod_{i=1}^n f(X_i | \theta)$

や，その対数を取った対数尤度関数を最大にするような $\theta = \hat{\theta}_{MLE}$ を求めるというものである。

具体的な解き方としては，尤度方程式

$\displaystyle \frac{\partial}{\partial \theta} L(\theta | X) = 0$

を $\theta$ について解き，得られた解を $\hat{\theta}_{MLE}$ とおくといったことが挙げられる。

一様分布のパラメータの最尤推定

一様分布

あらためて，一様分布の定義を確認する。確率変数 $X$ が閉区間 $[a, b ]$ 上の一様分布にしたがうとは， $X$ の確率密度関数が

\begin{equation}
f_X(x|a, b)=
\begin{cases}
1/(b - a) & \text{if $a \leq x \leq b$,} \\
0 & \text{otherwise}
\end{cases}
\end{equation}

で定義される。
今回は，パラメータが $\theta( \gt 0)$ のみの一様分布

\begin{equation}
f_X(x| \theta )=
\begin{cases}
1/ \theta & \text{if $0 \leq x \leq \theta$,} \\
0 & \text{otherwise}
\end{cases}
\end{equation}

を考えよう。

一様分布のパラメータの最尤推定 : 誤った手順

以下の流れは，私が初めてこの問題に対峙した時にしてしまったミスである。
一様分布の定義に沿って，尤度関数を考えると，

$\displaystyle L(\theta | X) = \prod_{i=1}^n f(X_i | \theta) = \theta ^{-n}$

となる。対数尤度関数は，

$\displaystyle l(\theta | X) = -n \log{\theta}$

となる。
パラメータ $\theta$ の最尤推定量を求める場合，対数尤度関数を最大にするような $\theta$ を求めればよいので，対数尤度関数を $\theta$ で微分したものを0とおいた尤度方程式を解けばよい。

$\displaystyle \frac{\partial}{\partial \theta} l(\theta | X) = \frac{\partial}{\partial \theta} (-n \log{\theta}) = - \frac{n}{\theta} = 0$

ここでミスに気付くのである。これでは， $\theta$ について解くことができない。

データの可視化

一様分布のパラメータの最尤推定に関する正しい手順を解説する前に，パラメータの推定値に当たりをつけてみよう。
データの可視化はデータサイエンスの基本なので，一様分布 $f(x|\theta) = U[0, \theta]$ について， $\theta = 1$ とした場合の確率密度関数と，この確率密度関数にしたがう乱数を図示してみよう。

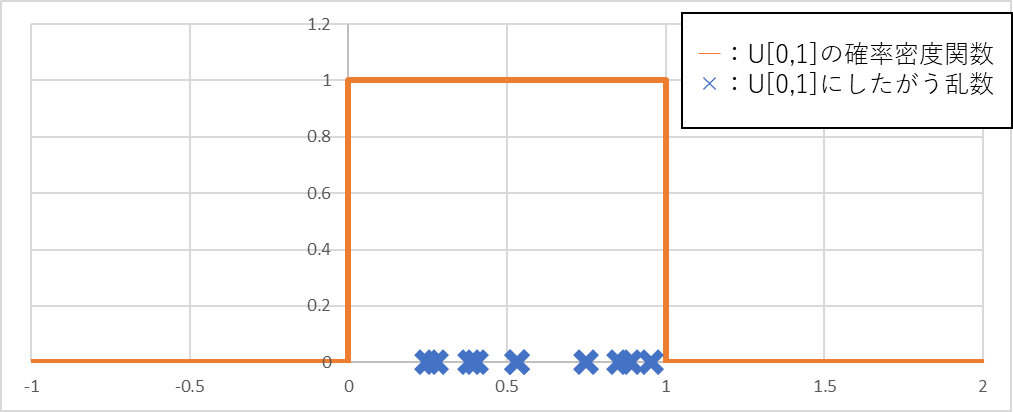
確率密度関数の形を見ると，値が $1/\theta$ から0に切り替わる点が $\theta$ である。また乱数は $[0, \theta]$ の範囲で発生するので，「発生した乱数のうち最大値である $X_{max}$ が $\theta$ に近い値になる」，すなわち「 $\theta$ の推定値は， $X_{max}$ である」と推察することができる。