「機械学習を解釈する技術」を読む　～第6章　予測の理由を考える ③SHapley Additive exPlanations～

はじめに

製造業の業務で機械学習モデルを運用する際に重要になる説明性・解釈性を把握するための手法を学ぶために，森下光之助著「機械学習を解釈する技術〜予測力と説明力を両立する実践テクニック」を読むことにした。

本記事は，「第6章　予測の理由を考える～SHapley Additive exPlanations～」における，SHAP(SHapley Additive exPlanations)値に関する読書メモである。

本書の紹介ページ

機械学習を解釈する技術〜予測力と説明力を両立する実践テクニック：書籍案内｜技術評論社

関連コード

GitHub - ghmagazine/ml_interpret_book

本記事を読むことで得られること

本記事では，以下のポイントについて説明する。

協力ゲーム理論におけるShapley値と，機械学習におけるSHAP値の関係
SHAP値の計算方法

6.4 SHapley Additive exPlanations

前節では，協力ゲーム理論におけるShapley値のコンセプトと，その計算手順を説明していた。本節ではShapley値のコンセプトを機械学習に応用し，特徴量の貢献度を計算する手法であるSHapley Additive exPlanations(SHAP)を説明している。

SHAPとShapley値の違い

機械学習におけるSHAPと，協力ゲームにおけるShapley値の違いは，限界貢献度の計算方法である。限界貢献度は，以下に示す特徴量 $j$ の貢献度 $\phi_j$ において，赤字部分である。

$\begin{align} \require{color} \phi_j = \frac{1}{\lvert \mathcal{J} \rvert} \sum_{\mathcal{S} \subseteq \mathcal{J} \backslash \{ j \}} (\lvert \mathcal{S} \rvert ! (\lvert \mathcal{J} \rvert - \lvert \mathcal{S} \rvert - 1)!) \times \textcolor{red}{(v(\mathcal{S} \cup \{ j\}) - v(\mathcal{S})) } \\ \end{align}$

「協力ゲーム理論におけるShapley値」の説明においては， $v(\mathcal{S} \cup \{ j\})$ などの報酬が事前に与えられていた。Shapley値を機械学習に応用する場合は，これらの値の計算方法を定義する必要がある。本書ではこの計算方法を，「特徴量 $j$ が分かっている場合と分かっていない場合での予測値の差分」と表現していたが，この「分かっている」・「分かっていない」という表現がピンとこなかったので整理してみた。

「特徴量が分かっている場合・分かっていない場合」の解釈

まず記号を再確認する。本書では特徴量を

$\begin{align} \boldsymbol{\mathrm{X}} = (X_1, ...., X_J) \\ \end{align}$

と表現している。この特徴量 $\boldsymbol{\mathrm{X}} = (X_1, ...., X_J)$ は，数理統計学における確率変数 $X$ のように，変数として扱われている。

一方で，学習データ・テストデータのように，値が確定したものはインスタンスと表現されている。 $N$ 個のインスタンスのうち， $i$ 番目のインスタンス(インスタンス $i$ )は，

$\begin{align} \boldsymbol{\mathrm{x}}_i = (x_{i,1}, ...., x_{i, J}) \\ \end{align}$

のように，表示される。特徴は，

特徴量は変数であり， $\boldsymbol{\mathrm{X}}$ のように大文字で表されている。
一方インスタンスは確定値であり， $\boldsymbol{\mathrm{x}}_i$ のように小文字で表されている。
インスタンスの要素は $x_{i, j}$ のように表されるが，インスタンスの番号の添え字は $i$ で，特徴量の番号の添え字は $j$ で表されている。

ということである。

学習済みモデル $\hat{f}$ と， $N$ 個のインスタンスからなるデータが揃っていれば，「特徴量が分かっていない」という状況は起きえないと思っていた。しかし本節の説明を読み進めると，

特徴量が分かっている : インスタンス $i$ の特徴量 $x_{i, j}$ の値を用いる。
特徴量が分かっていない : インスタンスの特徴量の値を用いない。
- その代わり，特徴量 $X_j$ の値は確定していないものとして周辺化，すなわち積分消去する(あるいは全てのインスタンスで平均を取る)。

という意味であると解釈できた。

具体例 : 特徴量が2つの場合

本項では具体例として，特徴量が $\boldsymbol{\mathrm{X}} = (X_1, X_2)$ で，インスタンス $i$ は $\boldsymbol{\mathrm{x}}_i = (x_{i, 1}, x_{i, 2})$ という値を取っているとする。

SHAPで最終的に行ないたいことは，

インスタンス $i$ の予測値 $\hat{f}(\boldsymbol{\mathrm{x}}_i ) = \hat{f}(x_{i, 1}, x_{i, 2})$ を，ベースライン $\phi_0$ および各特徴量の貢献度 $\phi_{i, 1}, \phi_{i, 2}$ で表す。

ということである(ICEと同様に，インスタンスごとに計算する)。

以下では，「全ての特徴量が変わっている場合」と「全ての特徴量が分かっていない場合」に分けて，Shapley値の計算における報酬 $v(\cdot)$ の計算方法を説明する。

全ての特徴量が分かっている場合

まずインスタンス $i$ における全ての特徴量 $\boldsymbol{\mathrm{x}}_i = (x_{i, 1}, x_{i, 2})$ が分かっているとする。この場合，Shapley値の計算における報酬 $v(\cdot)$ は，

$\begin{align} v(\{1, 2 \}) = \hat{f}(x_{i, 1}, x_{i, 2}) \\ \end{align}$

とすればよい。これは通常の機械学習タスクにおける，テストデータを用いた予測値の算出と同じである。

全ての特徴量が分かっていない場合

次に，特徴量が分かっていない場合について考える。この場合は，インスタンス $i$ の全ての特徴量 $\boldsymbol{\mathrm{x}}_i = (x_{i, 1}, x_{i, 2})$ は用いずに計算する(一部は用いることがある)。

インスタンスにおける特徴量の情報が全くない場合

インスタンスにおける特徴量の情報が全くない場合は，予測値の期待値を取る。すなわち，

$\begin{align} v( \emptyset ) = \mathbb{E} \left [ \hat{f}(X_1, X_2) \right ] \\ \end{align}$

とする。テストデータを用いて具体的に計算する場合は，全てのインスタンスについて予測値を計算し，その平均を取ればよい。

インスタンスにおける特徴量の情報の一部がない場合

特徴量 $X_1$ の値が分かっている，すなわちインスタンス $i$ における特徴量 $X_1$ の値が $x_{i, 1}$ であることが分かっているとする。逆に，特徴量 $X_2$ の値は分かっていない。

インスタンスにおける特徴量の情報が，一部が存在して一部がない場合は，存在していない特徴量について積分消去(または平均)すればよい。

$\begin{align} v( \{1\} ) &= \mathbb{E} \left [ \hat{f}(x_{i, 1}, X_2) \right ] = \int \hat{f}(x_{i, 1}, x_2) p(x_2) d x_2 \\ \end{align}$

この期待値を実測値から計算する場合， $x_{i, 1}$ は値が固定されているので，特徴量 $X_1$ に関しては全てのインスタンスで値を $x_{i, 1}$ で上書きし，全てのインスタンスに対して予測を行ない，これらの平均を計算する。

$\begin{align} \require{color} v( \{1\} ) &= \frac{1}{N} \sum_{i' = 1}^N \hat{f}( \textcolor{red}{x_{i, 1}} , x_{i', 2}) \\ \end{align}$

予測値の構成方法

上記を踏まえて， $x_{i, 1} \rightarrow x_{i, 2}$ の順で特徴量の値が分かった場合に予測値がどのように変化するかを確認する。

全ての特徴量が分かっていない → $x_{i, 1}$ のみが分かったときの予測値の変化

$\begin{align} \Delta_{i, 1} = \mathbb{E} \left[ \hat{f}(x_{i, 1}, X_2) \right] - \mathbb{E} \left[ \hat{f}(X_1, X_2) \right] \\ \end{align}$

$x_{i, 1}$ のみが分かっている → $(x_{i, 1}, x_{i, 2})$ が分かったときの予測値の変化

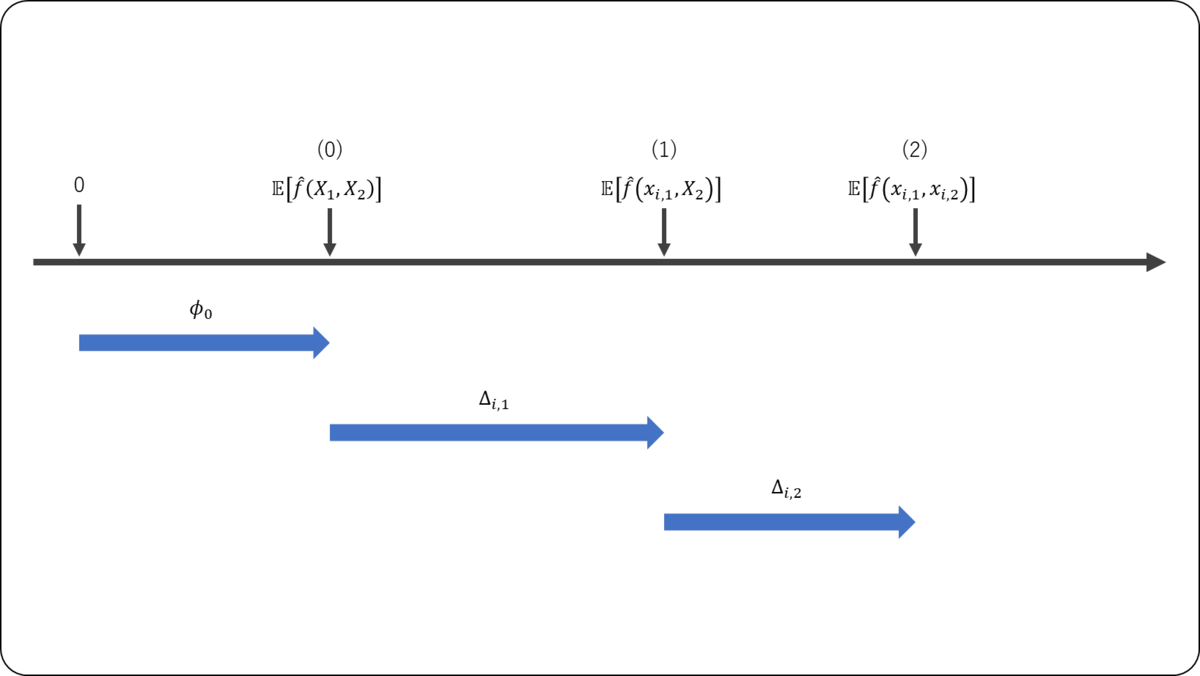
$\begin{align} \Delta_{i, 2} = \mathbb{E} \left[ \hat{f}(x_{i, 1}, x_{i, 2}) \right] - \mathbb{E} \left[ \hat{f}(x_{i, 1}, X_2) \right] \\ \end{align}$

特徴量の値が分かる順番の考慮

協力ゲーム理論におけるShapley値の計算では，順番を考慮することが重要であった。SHAPの計算においても同様に， $x_{i, 2} \rightarrow x_{i, 1}$ の順で特徴量の値が分かった場合では，各特徴量が予測値に与える影響が変化する。

考え得る全ての順序とその場合の予測値が与える影響は下表の通りである。

特徴量の値が分かった順番	$x_{i,1}$ が分かったことによる差分	$x_{i,2}$ が分かったことによる差分
$x_{i, 1} \rightarrow x_{i, 2}$	$\mathbb{E} \left[ \hat{f}(x_{i, 1}, X_{2}) \right] - \mathbb{E} \left[ \hat{f}(X_{1}, X_2) \right]$	$\mathbb{E} \left[ \hat{f}(x_{i, 1}, x_{i, 2}) \right] - \mathbb{E} \left[ \hat{f}(x_{i, 1}, X_2) \right]$
$x_{i, 2} \rightarrow x_{i, 1}$	$\mathbb{E} \left[ \hat{f}(x_{i, 1}, x_{i, 2}) \right] - \mathbb{E} \left[ \hat{f}(X_{1}, x_{i,2}) \right]$	$\mathbb{E} \left[ \hat{f}(X_{1}, x_{i, 2}) \right] - \mathbb{E} \left[ \hat{f}(X_{1}, X_2) \right]$

Shapley値の計算と同様に，SHAP値はそれぞれの特徴量が分かったことによる差分を平均すればよいので，以下のようになる。

$\begin{align} \phi_{i, 1} &= \frac{1}{2} \left( \mathbb{E} \left[ \hat{f}(x_{i, 1}, X_{2}) \right] - \mathbb{E} \left[ \hat{f}(X_{1}, X_2) \right] + \mathbb{E} \left[ \hat{f}(x_{i, 1}, x_{i, 2}) \right] - \mathbb{E} \left[ \hat{f}(X_{1}, x_{i,2}) \right] \right) \\ \\ \phi_{i, 2} &= \frac{1}{2} \left( \mathbb{E} \left[ \hat{f}(x_{i, 1}, x_{i, 2}) \right] - \mathbb{E} \left[ \hat{f}(x_{i, 1}, X_2) \right] + \mathbb{E} \left[ \hat{f}(X_{1}, x_{i, 2}) \right] - \mathbb{E} \left[ \hat{f}(X_{1}, X_2) \right] \right) \\ \end{align}$

更に上式からSHAP値 $\phi_{i, 1}, \phi_{i, 2}$ の合計は，

$\begin{align} \phi_{i, 1} + \phi_{i, 2} &= \hat{f}(x_{i, 1}, x_{i, 2}) - \mathbb{E} \left[ \hat{f}(X_1, X_2) \right] \\ \\ & \equiv \hat{f}(x_{i, 1}, x_{i, 2}) - \phi_0 \\ \end{align}$

となり，インスタンスの予測値は，ベースラインと各特徴量の貢献度の足し算に分解できることが分かる。