指数分布からの変換 #統計検定

はじめに

統計検定1級の統計数理・理工学において，指数分布は頻出分野である。この記事では，指数分布に関する話題のうち，指数分布から他の分布へ変換する，具体的には

指数分布→ガンマ分布・カイ2乗分布
指数分布→幾何分布

という変換について説明する。

指数分布への変換 #統計検定 - jiku log

はじめに
- 関連記事
- 目次
指数分布
- 統計検定1級での出題
指数分布と他の確率分布との関係
指数分布→ガンマ分布の変換
- 方針
- 導出
- 参考
指数分布→カイ2乗分布の変換
- 方針
- 導出
指数分布→幾何分布の変換
- 方針
- 導出
まとめ

指数分布

統計検定1級での出題

統計検定1級の統計数理・理工学において，2012年～2022年の10年の間で，関連する問題が8題出題されている。

指数分布と他の確率分布との関係

統計検定では，確率分布の性質，特に他の確率分布との関係を問われることが多い。指数分布と他の分布の関係は以下の通りである。

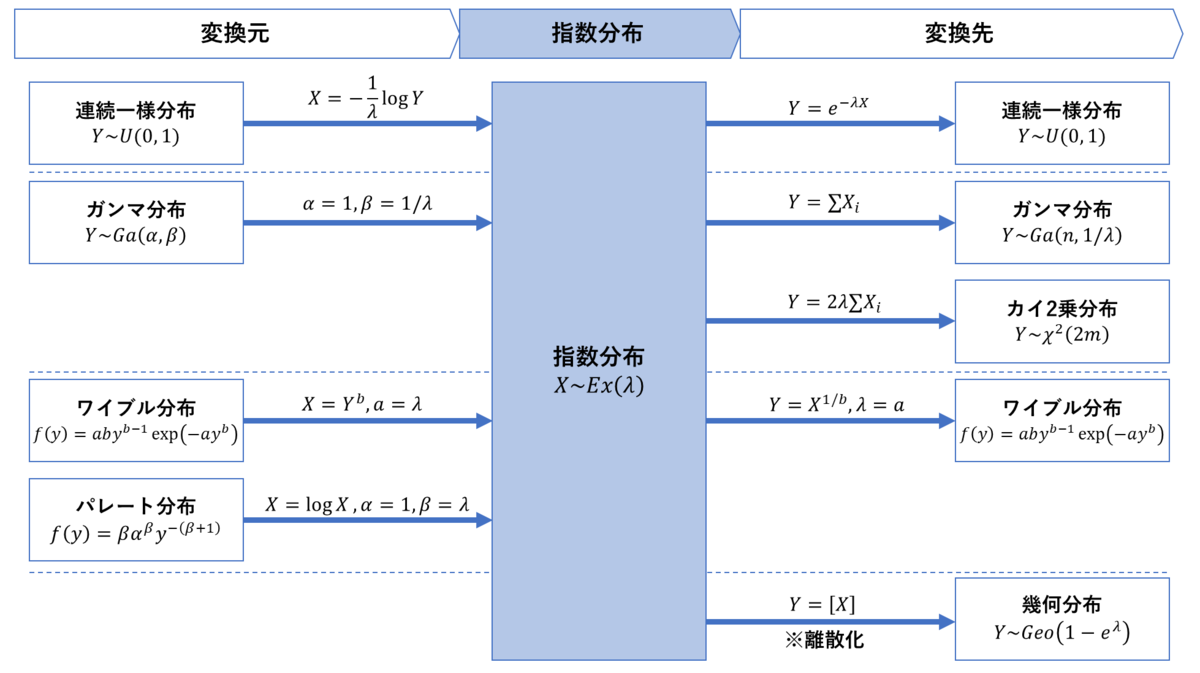
以下の説明では，確率変数 $X, Y$ の確率密度関数を $f_X(x), f_Y(y)$ とする。なお表記を簡単にするために，確率密度関数における定義域は略記する。

指数分布→ガンマ分布の変換

確率変数 $X$ が，指数分布 $Ex(\lambda)$ にしたがうとする。

$\displaystyle Y = \sum_{i=1}^{n} X_i$

という変換を行なうと，確率変数 $Y$ はガンマ分布にしたがう。

方針

導出にはモーメント母関数を用いる。
確率変数 $Y$ は確率変数 $X_i$ の和で表されているが，変数 $i$ にかかわらず確率変数 $X_i$ のモーメント母関数は同じ形になるうえに，モーメント母関数を用いると確率変数の和が積の形に変換できるので，モーメント母関数 $M_X(t)$ の $n$ 乗の形になり計算がしやすくなるためである。

なお，指数分布→ガンマ分布の変数変換は，ほかにも畳み込みを用いる方法などがある。

導出

指数分布 $Ex(\lambda)$ にしたがう確率変数 $X$ のモーメント母関数 $M_X(t)$ は，

$\displaystyle M_X(t) = E [ e^{tX} ] = \left( 1 - \frac{t}{\lambda} \right) ^{-1}$

である。また，確率変数 $Y$ のモーメント母関数 $M_Y(t)$ は，

$\displaystyle M_Y(t) = E [ \exp{( t \sum_{i=1}^{n} X_i )} ] = \prod_{i=1}^{n} E [ \exp{( t X_i )} ] = \left( 1 - \frac{t}{\lambda} \right) ^{-n}$

である。

ここで，ガンマ分布 $Ga(\alpha, \beta)$ にしたがう確率変数のモーメント母関数は $(1 - \beta t)^{- \alpha}$ なので， $M_Y(t)$ と比較すると， $Y$ はガンマ分布 $Ga(n, 1/\lambda)$ にしたがうことが分かる。

参考

指数分布 $Ex(\lambda)$ は，ガンマ分布 $Ga(1, 1/\lambda)$ と表される。上記より，指数分布にしたがう確率変数 $X$ を $n$ 回足し合わせると，ガンマ分布 $Ga(1, 1/\lambda)$ となることが分かる。このような性質をガンマ分布の再生性と呼ぶ。

ガンマ分布の再生性 :
確率変数 $S, T$ がそれぞれガンマ分布 $Ga(\alpha_1, \beta), Ga(\alpha_2, \beta)$ にしたがうとすると，確率変数 $S+T$ はガンマ分布 $Ga(\alpha_1 + \alpha_2, \beta)$ にしたがう。

指数分布→カイ2乗分布の変換

確率変数 $X$ が，指数分布 $Ex(\lambda)$ にしたがうとする。

$\displaystyle Y = 2 \lambda \sum_{i=1}^{m} X_i$

という変換を行なうと，確率変数 $Y$ はカイ2乗分布にしたがう。

方針

カイ2乗分布 $\chi ^2(n)$ はガンマ分布 $Ga(n/2, 2)$ に等しいので，ガンマ分布のときと同様にモーメント母関数を用いる。

導出

確率変数 $Y$ のモーメント母関数 $M_Y(t)$ は，

$\displaystyle M_Y(t) = E [ \exp{( 2 \lambda t \sum_{i=1}^{m} X_i )} ] = \prod_{i=1}^{m} E [ \exp{( 2 \lambda t X_i )} ]$

先に計算した，ガンマ分布のモーメント母関数の式と比べてみると， $t$ のかわりに $2 \lambda t$ を入れればよいことがわかる。よって，

$\displaystyle M_Y(t) = \prod_{i=1}^{m} E [ \exp{( 2 \lambda t X_i )} ] = \left( 1 - \frac{2 \lambda t}{\lambda} \right) ^{-m} = \left( 1 - 2 t \right) ^{-m}$

これは，ガンマ分布 $Ga(2m/2, 2)$ のモーメント母関数，すなわちカイ2乗分布 $\chi ^2(2m)$ のモーメント母関数であるので， $Y$ はカイ2乗分布 $\chi ^2(2m)$ にしたがう。

指数分布→幾何分布の変換

確率変数 $X$ が，指数分布 $Ex(\lambda)$ にしたがうとする。ガウス記号を用いて，

$\displaystyle Y = [ X]$

という変換を行なうと，確率変数 $Y$ は幾何分布にしたがう。

方針

はじめに気付くべき重要なこととして，確率変数 $X$ は連続分布にしたがうが，確率変数 $Y$ は離散分布にしたがうということである。

そのため，ヤコビアンを用いた変数変換のアプローチが取れない。したがって，連続分布と離散分布をつなぐものとして，累積分布関数と確率関数の関係に着目する。

導出

$\displaystyle Y = [ X] \Rightarrow Y \leq X \lt Y+1$

であるので，

$\begin{align} P(Y = k) &= P([X] = k) = P(k \leq X \lt k+1) \\ &= P(X \lt k+1) - P(X \lt k) \end{align}$

となる。
ここで，変数 $X$ は指数分布にしたがうので，その累積分布関数 $F_X(x) = P(X \lt x)$ は，

$\displaystyle F_X(x) = P(X \lt x) = 1 - e^{- \lambda x}$

となる。よって，

$\begin{align} P(Y = k) &= P(X \lt k+1) - P(X \lt k) \\ &= (1 - e^{- \lambda (k+1)} ) - (1 - e^{- \lambda k} ) \\ &= (e^{- \lambda})^k (1 - e^{- \lambda}) \end{align}$

となる。

さらに，