指数分布への変換 #統計検定

はじめに

統計検定1級の統計数理・理工学において，指数分布は頻出分野である。この記事では，指数分布に関する話題のうち，他の分布を指数分布へ変換する，具体的には

連続一様分布→指数分布
ガンマ分布→指数分布
ワイブル分布→指数分布
パレート分布→指数分布

という変換について説明する。

指数分布からの変換 #統計検定 - jiku log

指数分布

統計検定1級での出題

統計検定1級の統計数理・理工学において，2012年～2022年の10年の間で，関連する問題が8題出題されている。

指数分布と他の確率分布との関係

統計検定では，確率分布の性質，特に他の確率分布との関係を問われることが多い。指数分布と他の分布の関係は以下の通りである。

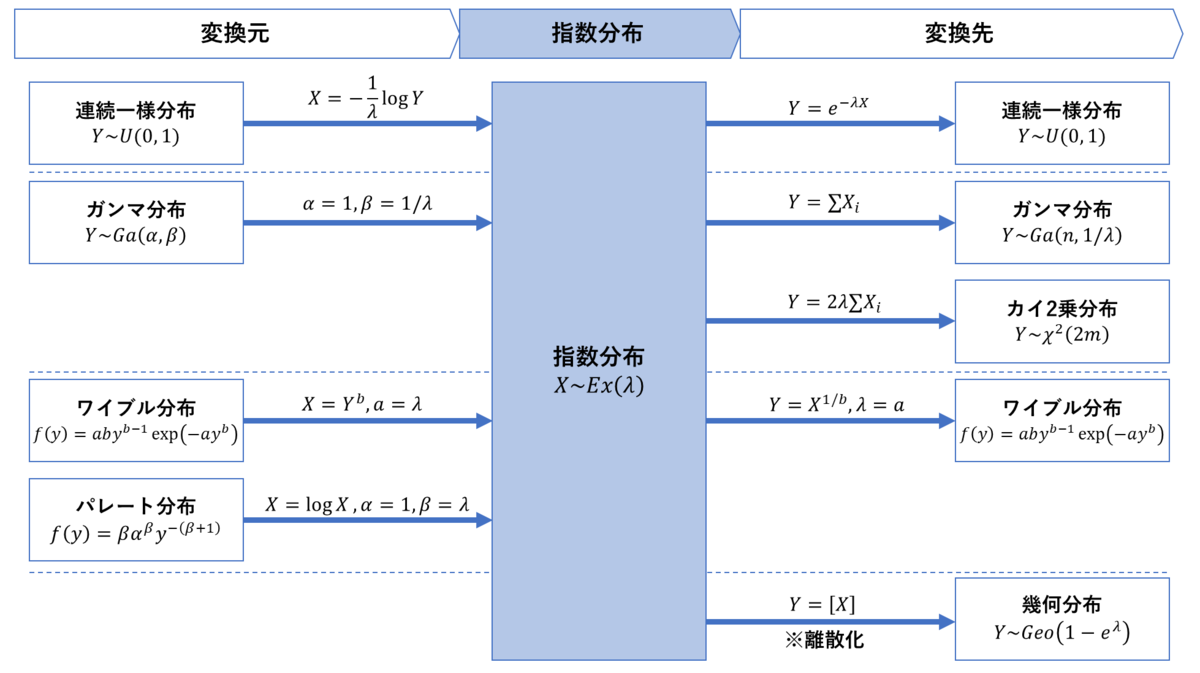
以下の説明では，確率変数 $X, Y$ の確率密度関数を $f_X(x), f_Y(y)$ とする。なお表記を簡単にするために，確率密度関数における定義域は略記する。

連続一様分布→指数分布の変換

確率変数 $Y$ が，連続一様分布 $U(0, 1)$ にしたがうとする。

$\displaystyle X = - \frac{1}{\lambda} \log Y \equiv g(Y)$

という変換を行なうと，確率変数 $X$ は指数分布にしたがう。

方針

連続一様分布には，変数が明示的に出てこないので，変数変換をして変数を出すためには，ヤコビアンに頼ることになる。

導出

$Y = - \frac{1}{\lambda} \log Y \Leftrightarrow Y = e^{- \lambda X}$ なので，ヤコビアンは $J$ は

$\displaystyle J = \left| \frac{dy}{dx} \right| = \left| - \lambda e^{- \lambda x} \right| = \lambda e^{- \lambda x}$

となる。
よって

$\displaystyle f_X(x) = f_Y(g^{-1}(x)) \left| \frac{dy}{dx} \right| = \lambda e^{- \lambda x}$

となり，指数分布が得られた。

ガンマ分布→指数分布の変換

確率変数 $Y$ が，ガンマ分布 $Ga(\alpha, \beta)$ にしたがうとする。

$\alpha = 1, \beta = 1/\lambda$ とすると，変換後の確率変数は指数分布にしたがう。

方針

ガンマ分布から指数分布への変換は，変数変換を用いない。すなわちガンマ分布の特殊ケースが指数分布である。

導出

$\displaystyle f_Y(y) = \frac{1}{\Gamma(\alpha) \beta ^ \alpha } y^{\alpha -1} e^{- \frac{y}{\beta}} \quad (x \gt 0)$

において， $\alpha = 1, \beta = 1/\lambda$ とする。 $\Gamma(1) = 0! = 1$ なので，

$\displaystyle f_Y(y) = \frac{1}{ 1/\lambda } e^{- \frac{y}{1/\lambda}} = \lambda e^{- \lambda y}$

となり，指数分布が得られた。

ワイブル分布→指数分布の変換

確率変数 $Y$ が，ワイブル分布 $Weibull(a, b) \quad (a \gt 0, b \gt 0)$ にしたがうとする。

$\displaystyle f_Y(y) = ab y^{b-1} \exp {(-a y^b)} \quad (x \gt 0)$

$X = Y^b, a = \lambda$ という変換を行なうと，確率変数 $X$ は指数分布にしたがう。

方針

変数変換の公式を淡々と当てはめていけば求められる。

導出

$X = Y^b \Leftrightarrow Y = X^{1/b}$ なので，ヤコビアンは $J$ は

$\displaystyle J = \left| \frac{dy}{dx} \right| = \frac{1}{b} x^{\frac{1}{b} - 1}$

となる。
よって

$\begin{align} f_X(x) &= f_Y(g^{-1}(x)) \left| \frac{dy}{dx} \right| = \lambda b (x^{\frac{1}{b}})^{b-1} \exp{(- \lambda x)} \times \frac{1}{b} x^{\frac{1}{b} - 1} \\ &= \lambda b x^{1 - \frac{1}{b}} \exp{(- \lambda x)} \times \frac{1}{b} x^{\frac{1}{b} - 1} \\ &= \lambda e^{- \lambda x} \end{align}$

となり，指数分布が得られた。

パレート分布→指数分布の変換

確率変数 $Y$ が，パレート分布 $Pareto(\alpha, \beta) \quad (\alpha \gt 0, \beta \gt 0)$ にしたがっているとする。

$\displaystyle f_Y(y) = \beta \alpha ^ \beta y^{-(\beta + 1)} \quad (x \gt 0)$

$X = \log{Y}, \alpha = 1, \beta=\lambda$ という変換を行なうと，確率変数 $X$ は指数分布にしたがう。

方針

変数変換の公式を淡々と当てはめていけば求められる。

導出

$X = \log{Y} \Leftrightarrow Y = e^X$ なので，ヤコビアンは $J$ は

$\displaystyle J = \left| \frac{dy}{dx} \right| = e^x$

となる。
よって

$\begin{align} f_X(x) &= f_Y(g^{-1}(x)) \left| \frac{dy}{dx} \right| = \lambda \exp{( -x(\lambda + 1) )} \times e^x \\ &= \lambda e^{- \lambda x} \end{align}$

となり，指数分布が得られた。