「Pythonではじめる時系列分析入門」を読む　～第4部第4章モデル選択～

はじめに

製造業におけるデータ分析において，時系列分析は重要かつ頻出課題の１つである。時系列分析の理論とPythonによる実装の両方を学ぶために，最近注目を集めている馬場真哉著　「Pythonではじめる時系列分析入門」を読むことにした。

本記事は，第4部「Box-Jenkins法とその周辺」の第4章「モデル選択」の読書メモである。

本書の紹介ページ

www.kspub.co.jp

第4部第4章モデル選択

SARIMAXモデルには，以下の7つのパラメータが存在する。

ARIMA過程のパラメータ : AR過程の次数 $p$ ，MA過程の次数 $q$ ，和分過程の次数 $d$
季節性に関するパラメータ : 周期 $m$ ，季節性に対するAR過程の次数 $P$ ，季節性に対するMA過程の次数 $Q$ ，季節和分過程の次数 $D$

本章では，これらのパラメータを選択するモデル選択の手続きについて説明している。

4.2 モデル選択の手続き

モデル選択の手続き手順は，下図の通りである。

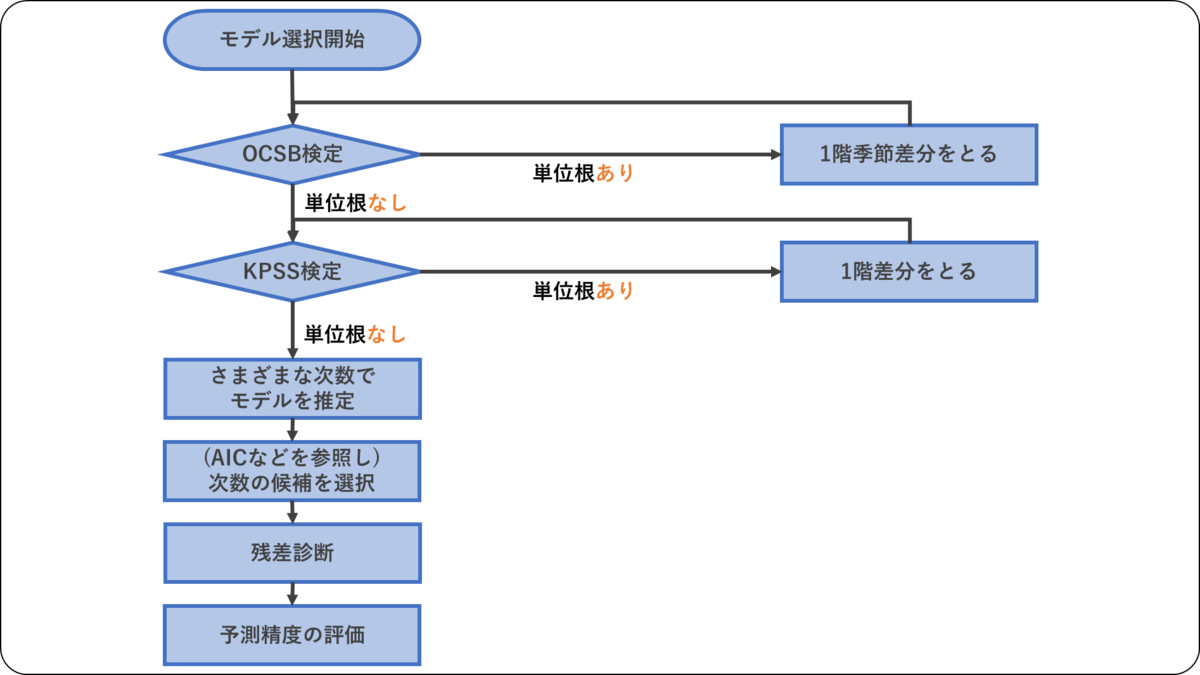
最初に，各種の単位根検定を行ない，差分を取る階数を決める。その後にAICによる次数選択，残差診断，予測精度の評価という手順で進める。

4.3 単位根検定 : DF検定とADF検定

差分をとる階数を決めるために，単位根検定を行なう。具体的な検定手順としては，DF検定やADF検定が存在する。

DF検定

DF検定はDickey-Fuller検定の略である。

検定の前提
- 1次のAR過程をデータ生成過程と想定する。
- $y_t = \phi_1 y_{t-1} + \varepsilon_t$
- ただし $\varepsilon_t \sim \mathrm{i.i.d}(0, \sigma^2)$ である。
帰無仮説
- $\phi_1 = 1$
対立仮説
- $\phi_1 \lt 1$

なお，帰無仮説が棄却できない場合，統計的仮説検定においては「帰無仮説は棄却できない」という判断にとどまるが，DF検定やADF検定では慣例として「単位根がある」と判断することが多いようである。

ADF検定

ADF検定(拡張DF検定，Augumented DF検定)は $p$ 次のAR過程を真のデータ生成過程と想定する検定である。ただしADF検定の場合，ARモデルの次数を決める必要があるので，本書では次節で紹介するKPSS検定を中心に利用することとしていた。

4.4 単位根検定 : KPSS検定

KPSS検定も単位根検定の手法であるが，前提としているデータ生成過程がDF検定などとは異なる。

検定の前提
- 以下のように，確定的トレンド $\beta t$ とランダムウォーク過程(第3項)が存在するデータ生成過程を想定する。
- $y_t = \alpha + \beta t + \sum_{i=1}^{t} u_i + \epsilon_t$
- ただし $u_i \sim \mathrm{i.i.d}(0, \sigma_u^2)$ であり， $\epsilon_t$ は定常過程である。
帰無仮説
- $\sigma_u^2 = 0$
対立仮説
- $\sigma_u^2 \neq 0$

帰無仮説が棄却された場合は，上記の慣例に沿って，単位根を持つ，と判断する。実際 $\sigma_u^2 = 0$ のとき，

$\begin{align} \Delta y_t = y_t - y_{t-1} = (\alpha + \beta t) - \{ \alpha + \beta (t - 1) \} = \beta \end{align}$

となる。

なお帰無仮説が正しいときのデータ系列は，定常過程ではなく「確定的トレンド+定常過程」となっている。

4.5 季節単位根検定 : DHF検定

DHF検定は季節単位根の有無を判断するための手法である。

検定の前提
- 1次の季節AR過程をデータ生成過程と想定する。
- $y_t = \Phi_1 y_{t-m} + \varepsilon_t$
- ただし周期は $m$ ， $\varepsilon_t \sim \mathrm{i.i.d}(0, \sigma^2)$ である。
帰無仮説
- $\Phi_1 = 1$
対立仮説
- $\Phi_1 \lt 1$

4.6 季節単位根検定 : OCSB検定

OCSB検定は，単位根と季節単位根の両方を持つ可能性があるデータ系列に適用する。

検定の前提
- 以下の回帰モデルをデータ生成過程と想定する。
- $\Delta \Delta_s y_t = \alpha \Delta_s y_{t-1} + \beta \Delta y_{t-m} + \varepsilon_t$
- ただし $\alpha, \beta$ は回帰係数， $\varepsilon_t \sim \mathrm{i.i.d}(0, \sigma^2)$ である。
帰無仮説
- $\beta = 1$
対立仮説
- $\beta \lt 1$

4.7 情報量規準

前節までは，単位根・季節単位根に関する検定であった。
本節からは，ARMAモデルの次数を決めるための方法である。

AIC

AIC(赤池情報量規準)はAkaike's Information Criterionの略であり，以下の式で定義される。

$\begin{align} \mathrm{AIC} = -2 \mathcal{L} + 2 \times \mathrm{n-params} \end{align}$

なお， $\mathcal{L}$ は最大化対数尤度， $\mathrm{n-params}$ は推定されたパラメータの個数である。

BIC

BIC(ベイズ情報量規準)はBayesian Information Criterionの略であり，以下の式で定義される。

$\begin{align} \mathrm{BIC} = -2 \mathcal{L} + \log{T} \times \mathrm{n-params} \end{align}$

なお， $\log{T}$ は訓練データのサンプル数であり，対数の底は自然定数である。サンプルサイズが8を超えると $\log{T} > 2$ となるので，BICの方がAICよりもパラメータ数の罰則が大きくなる。

AICとBICのどちらを用いるかは分析者が決めることになるが，本書ではAICを利用する。

4.8 残差診断と残差の可視化

前節まではモデルの「作成」について説明されていたが，本節ではモデルの「評価」について説明されている。

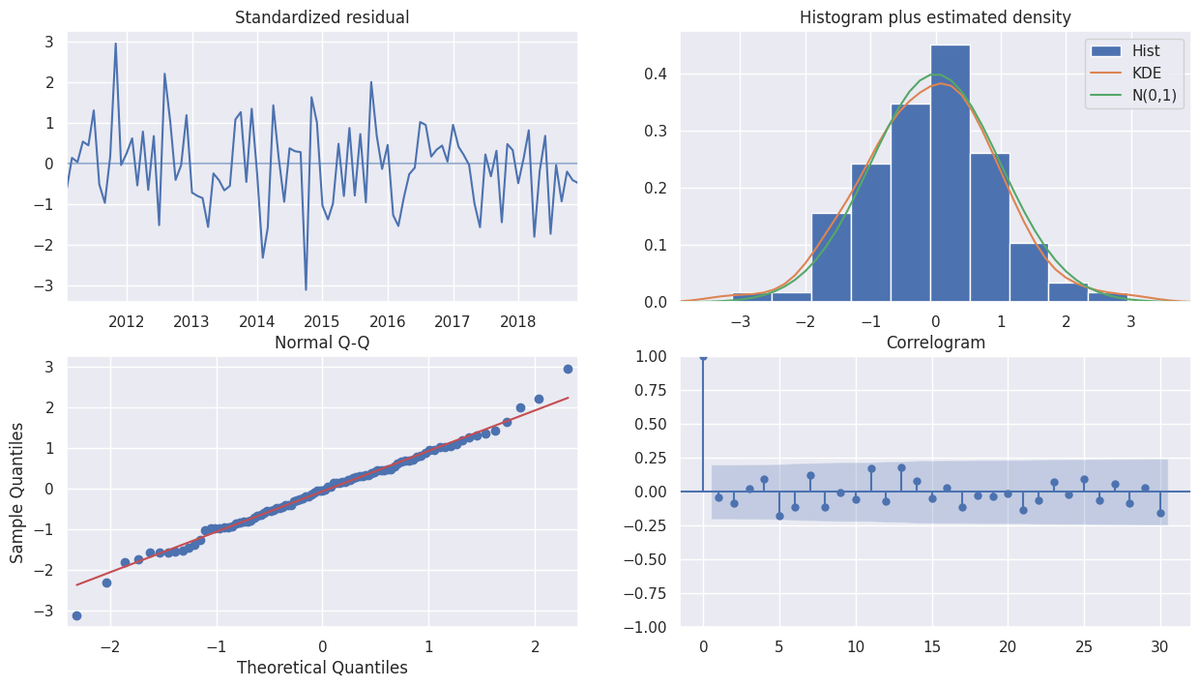
残差の評価には各種検定方法が存在するが，可視化を行なうことが重要である。主な可視化方法は以下の通りである。

残差の時系列折れ線グラフ : 外れ値の確認
残差のヒストグラム : 外れ値の確認
Q-Qプロット : 残差の正規性の確認
コレログラム : 残差の自己相関の確認

外れ値が学習データに存在すると，学習データの全体的な性質がモデルに反映されない(外れ値に影響を受ける)可能性がある。
Q-Qプロットは，「時系列モデルの誤差は正規性がある」という仮定を置いたモデルについて，その仮定が妥当であるかどうかを判断するために用いる。
コレログラムは，「残差には自己相関がない」という仮定を置いたモデルについて，その仮定が妥当であるかどうかを判断するために用いる。

まとめと感想

実業務への応用に向けて：モデルの妥当性を判断する力がより重要になる。

本章では，時系列モデルのモデル選択手順について丁寧にまとめられており，とても参考になった。またフローチャートで分析手順がまとめられているので，モデル作成がかなり自動化できると感じた。

ただ，このように「データが準備できれば，勝手に時系列モデルが作成される」という状況については，そのメリット・デメリットは把握するべきと感じた。

メリットは，自動化・プログラム化されているので，分析者の手間が省けることと，手順前後や各手順の誤りが減らせることである。手間や誤りが減れば，労働時間の削減につながりその分コストも減るので，会社にとっては生産性が上がるし，個人にとっては自分の余暇の時間が増えることにつながる。

一方でデメリットは，自動的に結果が出てしまうので，時系列モデルが誤っている場合に気付けずに使ってしまうことが考えられる。実業務で統計モデルや機械学習モデルを運用する際には，モデルについて理解し，説明できるようになっていることが求められることがある。手順を鵜呑みにしてしまうと，誤りに気付けない可能性がある。
また可視化を用いたモデルの評価についても，グラフを解釈して改善策を打てないといけないし，そのためには背景にある数理を理解することが重要になると感じた。

本記事を最後まで読んでくださり，どうもありがとうございました。